Phương trình tiếp tuyến
Phương trình tiếp tuyến là phương trình của một đường thẳng tiếp xúc với một đường cong tại một điểm cụ thể trên đường cong đó. Tiếp tuyến là đường thẳng chỉ chạm vào đường cong tại một điểm duy nhất và có cùng độ dốc với đường cong tại điểm tiếp xúc. Phương trình đường thẳng tiếp xúc mô tả cách mà các điểm trên đường thẳng này tương tác với đồ thị của hàm số tại điểm tiếp xúc.
Phương trình đường thẳng tiếp xúc được sử dụng để tìm các đường thẳng chạm vào đồ thị của hàm số tại một điểm cụ thể và có cùng hướng tại điểm đó. Đây là một công cụ quan trọng trong giải tích để nghiên cứu sự thay đổi của hàm số và phân tích các đặc điểm hình học của đồ thị.
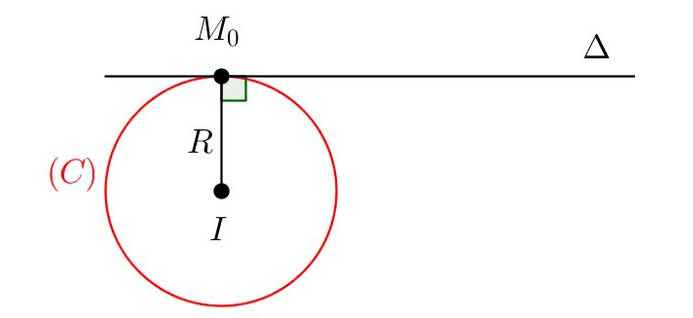
Định nghĩa về tiếp tuyếnĐể tìm phương trình đường thẳng tiếp xúc của một đường cong tại một điểm, bạn cần thực hiện các bước cơ bản sau:
Bước 1: Tính đạo hàm của hàm số
- Đạo hàm của hàm số f(x) là công cụ để tính độ dốc (hệ số góc) của tiếp tuyến tại một điểm cụ thể. Độ dốc này cho biết đường tiếp tuyến dốc lên hay dốc xuống tại điểm tiếp xúc.
- Giả sử bạn có một hàm số y=f(x), tính đạo hàm f′(x).
Bước 2: Tính hệ số góc của tiếp tuyến tại điểm đã cho
- Để tìm phương trình đường thẳng tiếp xúc tại điểm x₀, bạn cần tính đạo hàm tại điểm đó, tức là f'(x₀). Giá trị f'(x₀) chính là hệ số góc (độ dốc) của tiếp tuyến tại điểm (x₀, y₀), trong đó y₀ = f(x₀).
Bước 3: Sử dụng phương trình đường thẳng
Phương trình tổng quát của đường thẳng đi qua điểm (x₀, y₀) với hệ số góc m là: y − y₀ = m(x − x₀) Trong đó:
- m = f'(x₀) là hệ số góc của tiếp tuyến.
- (x₀, y₀) là tọa độ điểm tiếp xúc giữa tiếp tuyến và đường cong.
Bước 4: Viết phương trình đường thẳng tiếp xúc
- Thay giá trị m, x₀ và y₀ vào phương trình đường thẳng, bạn sẽ tìm được phương trình đường thẳng tiếp xúc.
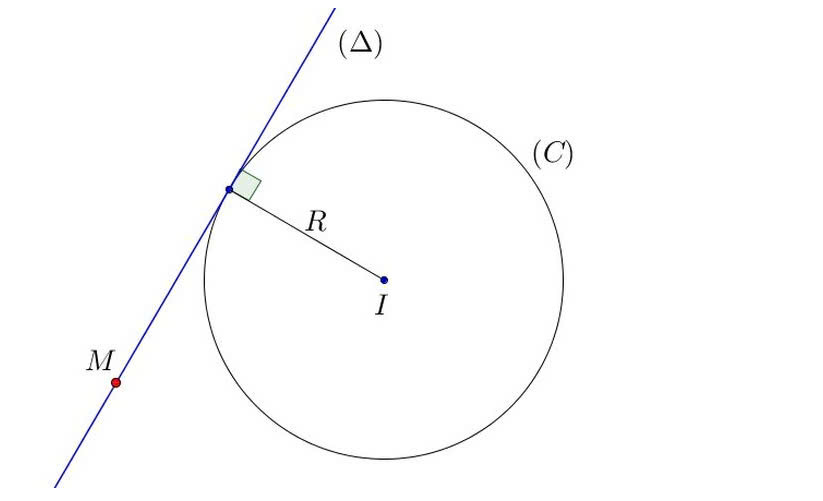
Ví dụ minh họaVí dụ minh họa
Giả sử bạn có hàm số y = f(x) = x², và bạn cần tìm phương trình đường thẳng tiếp xúc tại điểm (1,1).
Bước 1: Tính đạo hàm của hàm số
Bước 2: Tính hệ số góc tại điểm x=1
- f′(1)=2(1)=2
- Vậy, hệ số góc m=2.
Bước 3: Sử dụng phương trình đường thẳng
- Phương trình của đường thẳng tiếp tuyến là: y−1=2(x−1)
Bước 4: Viết phương trình đường thẳng tiếp xúc
Giải phương trình trên: y−1=2x−2
y=2x−1
Vậy, phương trình đường thẳng tiếp xúc của đồ thị y=x² tại điểm (1,1) là y=2x−1.

Công thức tổng quát của phương trình đường thẳng tiếp xúcCông thức tổng quát của phương trình đường thẳng tiếp xúc tại một điểm trên đồ thị của hàm số được mô tả như sau:
Công thức tổng quát
Giả sử y=f(x) là một hàm số liên tục và khả vi, và bạn muốn tìm phương trình đường thẳng tiếp xúc tại điểm (x₀, f(x₀)). Phương trình đường thẳng tiếp xúc có dạng:
- y = f'(x₀)(x - x₀) + f(x₀)
Trong đó:
- f'(x₀) là đạo hàm của hàm số f tại x0, đại diện cho hệ số góc (độ dốc) của tiếp tuyến.
- (x₀, f(x₀)) là tọa độ của điểm tiếp xúc giữa đường thẳng tiếp tuyến và đồ thị hàm số.
Tóm tắt:
- Hệ số góc của tiếp tuyến: m=f′(x0)
- Điểm tiếp xúc: (x₀, f(x₀))
Với công thức này, bạn có thể tính được phương trình đường thẳng tiếp xúc của bất kỳ hàm số nào tại một điểm cụ thể.

Các dạng bài tập về phương trình đường thẳng tiếp xúcDưới đây là một số dạng bài tập phổ biến về phương trình đường thẳng tiếp xúc cùng với hướng dẫn giải để giúp bạn hiểu rõ hơn về cách giải quyết từng dạng:
Tìm phương trình đường thẳng tiếp xúc tại một điểm cho hàm số
- Bài tập: Tìm phương trình đường thẳng tiếp xúc của hàm số f(x) = x³ - 3x + 1 tại điểm x₀ = 1.
- Hướng dẫn giải:
- Tính đạo hàm: f'(x) = 3x² - 3.
- Tính f'(1) = 3(1)² - 3 = 0 (hệ số góc).
- Tính f(1) = 1³ - 3(1) + 1 = -1 (điểm tiếp xúc).
- Phương trình đường thẳng tiếp xúc:y - (-1) = 0(x - 1) ⟹ y = -1
Tìm phương trình đường thẳng tiếp xúc song song với một đường thẳng cho trước
- Bài tập: Tìm phương trình đường thẳng tiếp xúc của hàm số f(x) = x² + 2x tại điểm có độ dốc bằng 4.
- Hướng dẫn giải:
- Tính đạo hàm: f′(x)=2x+2.
- Giải phương trình 2x+2=4 để tìm x: 2x=2 ⟹ x=1
- Tính điểm tiếp xúc: f(1) = 1² + 2(1) = 3.
- Phương trình đường thẳng tiếp xúc: y−3=4(x−1) ⟹ y=4x−1
Tìm phương trình đường thẳng tiếp xúc vuông góc với một đường thẳng cho trước
- Bài tập: Tìm phương trình đường thẳng tiếp xúc của hàm số f(x)=√x tại điểm mà tiếp tuyến vuông góc với đường thẳng y=2x+1.
- Hướng dẫn giải:
- Hệ số góc của đường thẳng cho trước là 2, do đó, hệ số góc của tiếp tuyến cần tìm là −1/2.
- Tính đạo hàm: f'(x) = 1/ 2√x .
- Giải phương trình 1/ 2√x = -1/2 không có nghiệm dương.
- Do đó, không có tiếp tuyến nào vuông góc với đường thẳng đó.
Tìm phương trình đường thẳng tiếp xúc cho đường tròn
- Bài tập: Tìm phương trình đường thẳng tiếp xúc của đường tròn có phương trình (x - 2)² + (y - 3)² = 9).
- Hướng dẫn giải:
- Điểm tiếp xúc là (2,6).
- Đường tròn có bán kính 3, do đó, tiếp tuyến sẽ có hệ số góc là 0 tại điểm đó.
- Phương trình đường thẳng tiếp xúc: y−6=0(x−2) ⟹ y=6
Tìm phương trình đường thẳng tiếp xúc của hàm số tại nhiều điểm
- Bài tập: Tìm phương trình đường thẳng tiếp xúc của hàm số f(x) = ln(x) tại x₁ = 1 và x₂ = e.
- Hướng dẫn giải:
- Tính đạo hàm: f′(x)=1/x.
- Tại x₁=1:
- f′(1)=1, f(1)=0.
- Phương trình: y−0=1(x−1) ⟹ y=x−1.
- Tại x₂=e:
- f′(e)=1/e, f(e)=1.
- Phương trình: y−1=1/e(x−e) ⟹ y=1/ex+(1−1).
Tìm tiếp tuyến chung của hai đường cong
- Bài tập: Tìm tiếp tuyến chung cho hai đường cong y = x² và y = x + 1.
- Hướng dẫn giải:
- Tìm đạo hàm của từng hàm.
- Giải hệ phương trình với độ dốc và điểm tiếp xúc cho cả hai hàm để tìm tiếp tuyến chung.
Các ví dụ trên đã cho thấy sự đa dạng và phong phú của ứng dụng phương trình đường thẳng tiếp xúc. Điều này không chỉ giúp ích cho việc học tập mà còn trang bị cho chúng ta những kỹ năng cần thiết để giải quyết các bài toán phức tạp hơn trong tương lai. Hi vọng rằng những kiến thức và phương pháp đã được trình bày sẽ là nền tảng vững chắc cho việc nghiên cứu và khám phá sâu hơn về các khái niệm hình học và giải tích trong toán học.
Ngoài ra, nếu bạn có nhu cầu về dịch vụ chống thấm dột, sơn sửa nhà cũ, hãy liên hệ với chúng tôi để được tư vấn nhé!
Công ty cổ phần Xây dựng và Công nghệ SCT Việt Nam
Địa chỉ: Số 15 - Ngõ 466 - Hoàng Hoa Thám - Tây Hồ - Hà Nội
Hotline: 0974.927.004
Email: xaydungsct@gmail.com
Website: http://www.chongthamsct.vn/