Phương trình tiếp tuyến
Phương trình tiếp tuyến là gì?
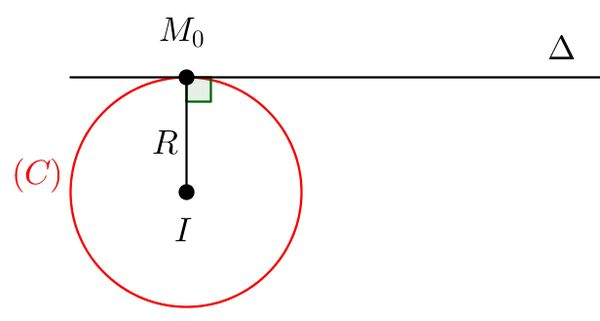
Phương trình đường tiếp tuyến là phương trình của một đường thẳng tiếp xúc với đồ thị của một hàm số tại một điểm cụ thể. Nói cách khác, tiếp tuyến là đường thẳng "chạm" vào đồ thị hàm số tại một điểm và có cùng hướng với đồ thị hàm số tại điểm đó.
Ý nghĩa hình học
Tiếp xúc tại một điểm: Tiếp tuyến chỉ cắt đồ thị hàm số tại một điểm duy nhất, gọi là tiếp điểm.
Cùng hướng: Tại tiếp điểm, tiếp tuyến có cùng hướng với đồ thị hàm số, nghĩa là hệ số góc của tiếp tuyến bằng đạo hàm của hàm số tại điểm tiếp xúc.
Công thức chung
Giả sử ta có hàm số y = f(x) và điểm M(x₀, y₀) thuộc đồ thị hàm số. Khi đó, phương trình đường tiếp tuyến tại điểm M có dạng:
y = f'(x₀)(x - x₀) + y₀
Trong đó:
- f'(x₀) là đạo hàm của hàm số f(x) tại điểm x₀, đồng thời cũng là hệ số góc của tiếp tuyến.
- (x₀, y₀) là tọa độ của tiếp điểm.
Các bước viết phương trình đường tiếp tuyến
Tìm đạo hàm: Tính đạo hàm của hàm số f(x).
Tìm hệ số góc: Tính giá trị của đạo hàm tại điểm x₀ để tìm hệ số góc của tiếp tuyến.
Viết phương trình: Thay các giá trị tìm được vào công thức chung để viết phương trình đường tiếp tuyến.
Ví dụ
Cho hàm số y = x² và điểm M(2, 4) thuộc đồ thị. Viết phương trình đường tiếp tuyến tại M.
Bước 1: Tính đạo hàm: y' = 2x.
Bước 2: Tìm hệ số góc: Tại x = 2, y' = 2*2 = 4.
Bước 3: Viết phương trình: y = 4(x - 2) + 4 => y = 4x - 4.
Vậy phương trình đường tiếp tuyến của đồ thị hàm số y = x² tại điểm M(2, 4) là y = 4x - 4.
Ứng dụng
Tìm cực trị: Tiếp tuyến tại điểm cực trị của đồ thị hàm số có hệ số góc bằng 0.
Xấp xỉ hàm số: Trong một khoảng nhỏ xung quanh tiếp điểm, tiếp tuyến có thể được sử dụng để xấp xỉ giá trị của hàm số.
Giải các bài toán liên quan đến đồ thị hàm số: Tìm giao điểm của tiếp tuyến với các đường thẳng khác, tìm khoảng cách từ một điểm đến tiếp tuyến, …
>> Xem thêm: Công thức tính công suất
Phương trình đường tiếp tuyếnViết phương trình tiếp tuyến tại một điểm cho trước trên đồ thị:
Cho: Hàm số y = f(x) và một điểm M(x₀, y₀) thuộc đồ thị.
Yêu cầu: Viết phương trình đường tiếp tuyến tại điểm M.
Cách giải:
- Tính đạo hàm f'(x).
- Tính hệ số góc k = f'(x₀).
- Viết phương trình đường tiếp tuyến: y = k(x - x₀) + y₀.
Viết phương trình đường tiếp tuyến biết tiếp tuyến đi qua một điểm cho trước
Cho: Hàm số y = f(x) và một điểm A không thuộc đồ thị.
Yêu cầu: Viết phương trình tiếp tuyến của đồ thị hàm số đi qua điểm A.
Cách giải:
- Giả sử tiếp điểm là M(x₀, y₀).
- Viết phương trình đường tiếp tuyến tổng quát: y = k(x - x₀) + y₀.
- Thay tọa độ điểm A vào phương trình đường tiếp tuyến, ta được một phương trình ẩn x₀.
- Giải phương trình để tìm x₀, từ đó tìm được y₀ và k.
Tìm các tiếp tuyến của đồ thị hàm số song song hoặc vuông góc với một đường thẳng cho trước
Cho: Hàm số y = f(x) và một đường thẳng d: y = ax + b.
Yêu cầu: Tìm các tiếp tuyến của đồ thị hàm số song song hoặc vuông góc với đường thẳng d.
Cách giải:
- Tính hệ số góc k của đường thẳng d.
- Nếu tìm tiếp tuyến song song: Giải phương trình f'(x) = k.
- Nếu tìm tiếp tuyến vuông góc: Giải phương trình f'(x) = -1/k.
- Tìm các tiếp điểm tương ứng và viết phương trình đường tiếp tuyến.
Tìm các tiếp tuyến của đồ thị hàm số có hệ số góc cho trước
Cho: Hàm số y = f(x) và một giá trị k.
Yêu cầu: Tìm các tiếp tuyến của đồ thị hàm số có hệ số góc bằng k.
Cách giải:
- Giải phương trình f'(x) = k.
- Tìm các tiếp điểm tương ứng và viết phương trình đường tiếp tuyến.
Các bài toán liên quan đến tiếp tuyến và cực trị
Tìm tiếp tuyến tại điểm cực trị của đồ thị hàm số.
Tìm các tiếp tuyến của đồ thị hàm số đi qua gốc tọa độ.
Tìm các tiếp tuyến của đồ thị hàm số cắt trục Ox, Oy tại các điểm có hoành độ, tung độ cho trước.
Phương trình đường tiếp tuyếnBài tập 1: Cấp độ cơ bản
Cho hàm số y = x² + 2x - 1. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = 1.
Bài tập 2: Cấp độ trung bình
Tìm tất cả các giá trị của tham số m để đường thẳng y = mx + 2 tiếp xúc với đồ thị hàm số y = x² - 2x + 3.
Bài tập 3: Cấp độ nâng cao
Cho hàm số y = x³ - 3x. Viết phương trình các tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng y = 9x - 15.
Phương trình đường tiếp tuyếnBài tập 1:
Tính đạo hàm: y' = 2x + 2.
Tại x = 1, ta có y'(1) = 4.
Khi x = 1, y = 1² + 2*1 - 1 = 2.
Phương trình đường tiếp tuyến: y = 4(x - 1) + 2 hay y = 4x - 2.
Bài tập 2:
Để đường thẳng tiếp xúc với đồ thị hàm số thì hệ phương trình sau phải có nghiệm kép: y = mx + 2 y = x² - 2x + 3
Giải hệ phương trình trên, ta được phương trình bậc hai: x² - (m+2)x + 1 = 0.
Để phương trình có nghiệm kép thì Δ = (m+2)² - 4 = 0.
Giải phương trình trên, ta tìm được m = 0 hoặc m = -4.
Bài tập 3:
Tính đạo hàm: y' = 3x² - 3.
Để tiếp tuyến song song với đường thẳng y = 9x - 15 thì hệ số góc của tiếp tuyến bằng 9.
Giải phương trình: 3x² - 3 = 9, ta được x = ±2.
Khi x = 2, y = 2. Phương trình đường tiếp tuyến: y = 9(x - 2) + 2 hay y = 9x - 16.
Khi x = -2, y = -2. Phương trình đường tiếp tuyến: y = 9(x + 2) - 2 hay y = 9x + 16.
Trên đây là một số thông tin về chủ đề viết phương trình đường tiếp tuyến. Hi vọng các bạn sẽ có cho mình thông tin hữu ích.