Diện tích mặt cầu
Mặt cầu là gì?
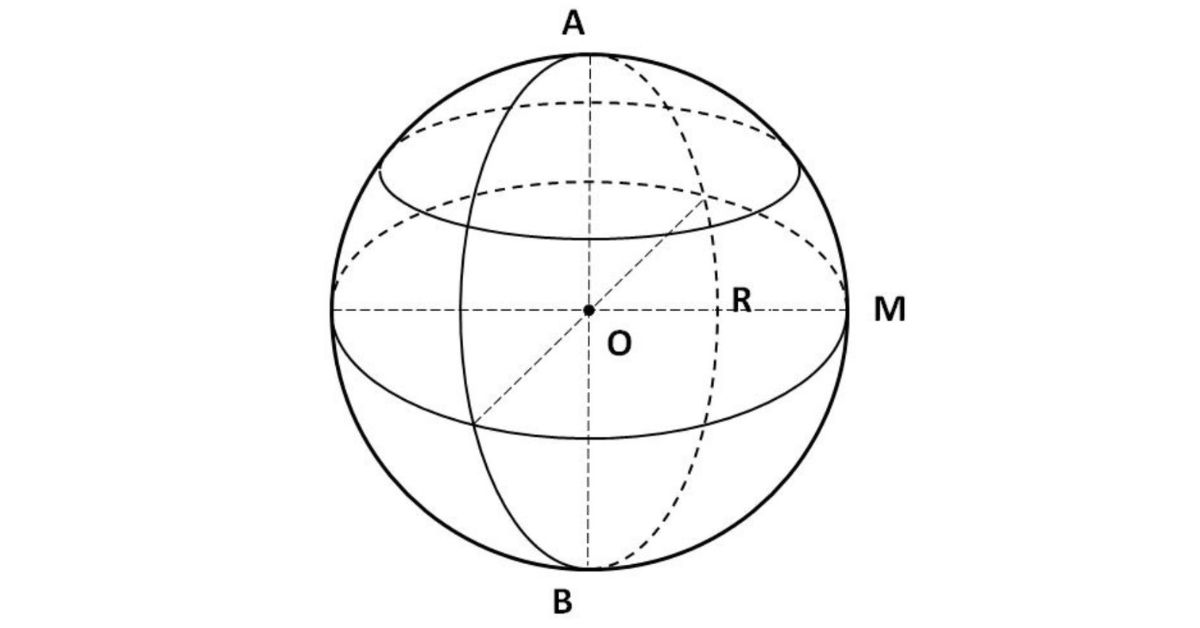
Định nghĩa: Mặt cầu là tập hợp tất cả các điểm trong không gian cách đều một điểm cố định O cho trước một khoảng cách không đổi R. Điểm O được gọi là tâm của mặt cầu, còn khoảng cách R được gọi là bán kính của mặt cầu.
Hình dung: Bạn có thể hình dung mặt cầu như một quả bóng bóng căng tròn. Bất kỳ điểm nào trên bề mặt quả bóng đều cách tâm của quả bóng một khoảng bằng nhau.
Tính chất: Mặt cầu là một hình đối xứng hoàn hảo. Dù bạn xoay mặt cầu theo bất kỳ góc nào, nó vẫn giữ nguyên hình dạng.
Hình cầu là gì?
Định nghĩa: Hình cầu là phần không gian bên trong mặt cầu. Nói cách khác, hình cầu là tập hợp tất cả các điểm có khoảng cách đến tâm mặt cầu nhỏ hơn hoặc bằng bán kính.
Ví dụ: Một quả bóng bàn là một ví dụ về hình cầu. Bề mặt của quả bóng bàn là mặt cầu, còn phần bên trong quả bóng bàn là hình cầu.
Sự khác biệt giữa hình cầu và mặt cầu
Mặt cầu: Chỉ là bề mặt bên ngoài, giống như vỏ của một quả bóng.
Hình cầu: Bao gồm cả bề mặt và phần bên trong, giống như toàn bộ quả bóng.

Hình cầu và mặt cầuTrong cuộc sống hàng ngày
Sản xuất:
Quả bóng: Để sản xuất quả bóng đạt tiêu chuẩn, các nhà sản xuất cần tính toán chính xác diện tích bề mặt để đảm bảo lượng da hoặc vật liệu phủ đủ dùng.
Bóng đèn: Diện tích bề mặt của bóng đèn ảnh hưởng trực tiếp đến lượng ánh sáng phát ra.
Các vật dụng hình cầu khác: Từ bình cầu, quả địa cầu cho đến các loại đồ chơi, việc tính toán diện tích giúp tối ưu hóa vật liệu và chi phí sản xuất.
Xây dựng:
Mái vòm: Diện tích mái vòm giúp tính toán lượng vật liệu cần thiết để lợp mái, đồng thời đảm bảo độ bền và khả năng chống thấm.
Bể chứa: Diện tích bề mặt của bể chứa giúp tính toán lượng sơn cần thiết để bảo vệ bề mặt, cũng như lượng nhiệt cần thiết để làm nóng hoặc làm lạnh nước.
Nông nghiệp:
Tưới tiêu: Diện tích bề mặt của các hệ thống tưới tiêu dạng phun sương giúp xác định lượng nước cần thiết để tưới cho cây trồng.
Phun thuốc: Diện tích bề mặt của các loại trái cây giúp tính toán lượng thuốc trừ sâu cần thiết để bảo vệ cây trồng.
Trong khoa học và kỹ thuật
Vật lý:
Tính toán lực cản: Diện tích bề mặt của một vật thể ảnh hưởng đến lực cản của nó khi di chuyển trong chất lỏng hoặc khí.
Tính toán nhiệt lượng: Diện tích bề mặt của một vật thể ảnh hưởng đến tốc độ truyền nhiệt của nó.
Thiên văn học:
Tính toán diện tích bề mặt các hành tinh: Giúp chúng ta so sánh kích thước và khối lượng của các hành tinh.
Tính toán lượng bức xạ: Diện tích bề mặt của một hành tinh ảnh hưởng đến lượng bức xạ mặt trời mà nó hấp thụ.
Kỹ thuật hàng không vũ trụ:
Thiết kế vệ tinh: Diện tích bề mặt của vệ tinh ảnh hưởng đến khả năng hấp thụ và phát xạ nhiệt, cũng như khả năng chống chịu các tác động từ môi trường không gian.
Tính toán lực cản: Diện tích bề mặt của tàu vũ trụ ảnh hưởng đến lực cản khi nó di chuyển trong khí quyển.
>> Xem thêm: Cách viết bản kiểm điểm
Hình cầuMối liên hệ giữa diện tích và thể tích
Chúng ta có thể rút ra một số kết luận thú vị về mối liên hệ giữa diện tích và thể tích của hình cầu:
Tỷ lệ giữa diện tích và thể tích: Khi bán kính của hình cầu tăng lên, tỷ lệ giữa diện tích và thể tích sẽ giảm dần. Điều này giải thích tại sao các vật thể có kích thước nhỏ hơn thường có tỷ lệ diện tích bề mặt trên thể tích lớn hơn so với các vật thể có kích thước lớn hơn.
Ứng dụng trong thực tế: Hiểu rõ mối liên hệ này giúp chúng ta giải thích nhiều hiện tượng trong tự nhiên và cuộc sống. Ví dụ, các tế bào có hình cầu để tăng cường quá trình trao đổi chất, bong bóng xà phòng có hình cầu để giảm diện tích bề mặt tiếp xúc với không khí, giúp chúng ổn định hơn.
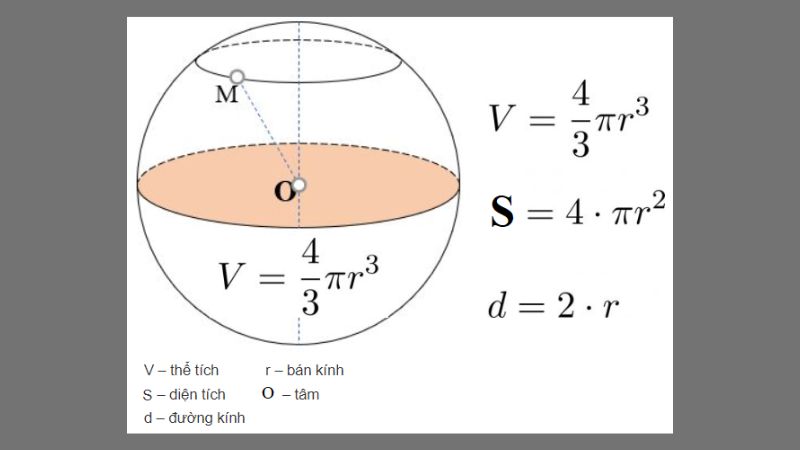
Để tính toán diện tích và thể tích của hình cầu, chúng ta cần nắm vững một số công thức sau:
Bán kính (r): Khoảng cách từ tâm hình cầu đến bất kỳ điểm nào trên bề mặt hình cầu.
Đường kính (d): Độ dài của một đoạn thẳng đi qua tâm hình cầu và có hai đầu mút nằm trên bề mặt hình cầu. Lưu ý: d = 2r.
Số Pi (π): Một hằng số toán học đặc biệt, xấp xỉ bằng 3.14.
Công thức tính diện tích mặt cầu:
S = 4πr² hoặc S = πd²
Trong đó:
S: Diện tích mặt cầu
r: Bán kính hình cầu
d: Đường kính hình cầu
Công thức tính thể tích khối cầu:
V = (4/3)πr³
Trong đó:
V: Thể tích khối cầu
r: Bán kính hình cầu
Giải thích ý nghĩa của các công thức
Diện tích mặt cầu: Công thức này cho biết tổng diện tích bề mặt của hình cầu. Hãy tưởng tượng bạn muốn sơn một quả bóng, thì diện tích cần sơn chính là diện tích mặt cầu đó.
Thể tích khối cầu: Công thức này cho biết lượng không gian mà hình cầu chiếm giữ. Ví dụ, nếu bạn muốn đổ đầy nước vào một quả bóng rỗng, thì thể tích nước đó chính là thể tích khối cầu.
Ví dụ minh họa
Giả sử bạn có một quả bóng có bán kính là 5cm. Để tính diện tích và thể tích của quả bóng này, bạn thực hiện như sau:
Diện tích: S = 4π x 5² ≈ 314 cm²
Thể tích: V = (4/3)π x 5³ ≈ 524 cm³
Các công thức liên quan đến mặt cầuTrên đây là các thông tin về chủ đề diện tích mặt cầu. Hi vọng các bạn đã có cho mình thông tin hữu ích.
>> Tham khảo: Thợ chống thấm hà nội