Phương trình tiếp tuyến
Phương trình tiếp tuyến là một khái niệm quan trọng trong toán học, đặc biệt là trong môn Giải tích. Nó đại diện cho một đường thẳng chạm vào đồ thị của một hàm số tại một điểm cụ thể, và tại điểm chạm đó, đường thẳng và đồ thị hàm số có cùng hướng.
Công thức chung
Phương trình đường tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = x₀ là:
y = f'(x₀)(x - x₀) + f(x₀)
Trong đó:
f'(x₀): Là đạo hàm của hàm số f(x) tại điểm x = x₀, đại diện cho hệ số góc của tiếp tuyến.
(x - x₀): Là khoảng cách theo trục hoành từ điểm tiếp xúc đến một điểm bất kỳ trên tiếp tuyến.
f(x₀): Là tung độ của điểm tiếp xúc.
Ý nghĩa
Hệ số góc: Cho biết độ dốc của tiếp tuyến tại điểm tiếp xúc.
Điểm tiếp xúc: Xác định vị trí chính xác mà tiếp tuyến chạm vào đồ thị hàm số.
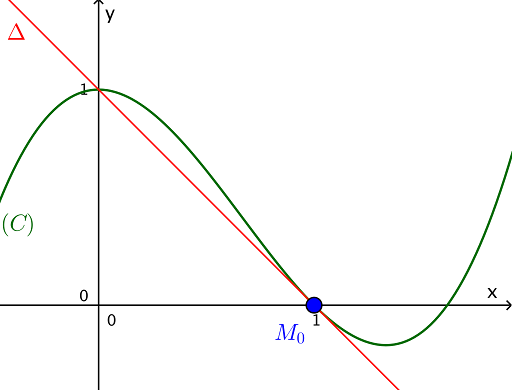
Phương trình đường tiếp tuyếnViết phương trình tiếp tuyến của đồ thị hàm số tại một điểm cho trước
Cách giải:
Tính đạo hàm của hàm số tại điểm đó để tìm hệ số góc của tiếp tuyến.
Thay tọa độ điểm tiếp xúc vào công thức tổng quát của phương trình đường thẳng để tìm phương trình tiếp tuyến.
Viết phương trình đường tiếp tuyến của đồ thị hàm số biết tiếp tuyến đi qua một điểm
Cách giải:
Giả sử phương trình đường tiếp tuyến có dạng y = kx + b.
Tìm mối liên hệ giữa k và b bằng cách sử dụng điều kiện tiếp tuyến đi qua điểm cho trước.
Giải hệ phương trình để tìm k và b.
Tìm điểm trên đồ thị hàm số sao cho tiếp tuyến thỏa mãn điều kiện cho trước
Cách giải:
Giả sử điểm cần tìm có tọa độ (x₀, y₀).
Viết phương trình đường tiếp tuyến tại điểm đó.
Lập phương trình dựa trên điều kiện cho trước (ví dụ: tiếp tuyến vuông góc với một đường thẳng, tiếp tuyến đi qua gốc tọa độ,...)
Giải hệ phương trình để tìm x₀ và y₀.
Tìm các giá trị của tham số m để đồ thị hàm số có tiếp tuyến thỏa mãn điều kiện cho trước
Cách giải:
Viết phương trình đường tiếp tuyến chung.
Lập phương trình dựa trên điều kiện cho trước (ví dụ: tiếp tuyến song song với một đường thẳng, tiếp tuyến cắt trục Ox tại một điểm có hoành độ dương,...)
Giải phương trình để tìm các giá trị của tham số m.
Các bài toán liên quan đến tiếp tuyến và cực trị
Cách giải:
Tìm các điểm cực trị của hàm số.
Viết phương trình đường tiếp tuyến tại các điểm cực trị.
Sử dụng các kiến thức về cực trị để giải quyết bài toán.
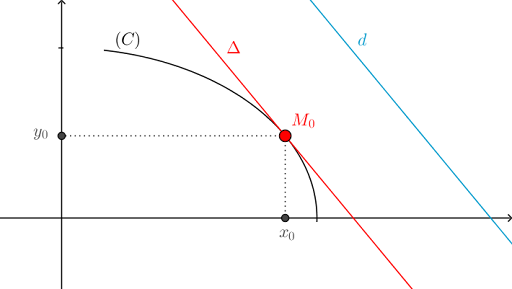
Phương trình đường tiếp tuyếnVật lý
Chuyển động:
- Vận tốc tức thời: Đạo hàm của quãng đường theo thời gian chính là vận tốc tức thời tại một thời điểm cụ thể. Vận tốc tức thời này chính là hệ số góc của tiếp tuyến với đồ thị quãng đường - thời gian tại điểm thời gian đó.
- Gia tốc tức thời: Đạo hàm của vận tốc theo thời gian chính là gia tốc tức thời. Tương tự, gia tốc tức thời cũng có thể được hiểu qua hệ số góc của tiếp tuyến với đồ thị vận tốc - thời gian.
Điện học:
- Dòng điện tức thời: Trong mạch điện xoay chiều, cường độ dòng điện biến thiên theo thời gian. Đạo hàm của cường độ dòng điện tại một thời điểm cho ta giá trị tức thời của dòng điện tại thời điểm đó.
Kinh tế
- Tốc độ tăng trưởng: Đạo hàm của hàm cầu hoặc hàm cung tại một điểm cho biết tốc độ thay đổi của cầu hoặc cung khi giá cả thay đổi. Điều này giúp các nhà kinh tế dự đoán xu hướng thị trường.
- Lợi nhuận biên: Đạo hàm của hàm lợi nhuận tại một mức sản lượng cho biết lợi nhuận thu được thêm khi tăng thêm một đơn vị sản lượng.
Kỹ thuật
Xây dựng:
- Độ dốc của mái nhà: Độ dốc của mái nhà tại một điểm chính là hệ số góc của tiếp tuyến với mặt cắt của mái nhà tại điểm đó.
- Độ cong của cầu: Độ cong của cầu tại một điểm cũng được xác định bằng hệ số góc của tiếp tuyến.
Máy móc:
- Vận tốc của các bộ phận chuyển động: Vận tốc của các bộ phận chuyển động trong máy móc thường được mô hình hóa bằng các hàm số. Đạo hàm của các hàm số này cho ta vận tốc tức thời của các bộ phận đó.
Hình học
Tìm điểm cực trị của đồ thị hàm số: Tiếp tuyến tại điểm cực trị của đồ thị hàm số có hệ số góc bằng 0.
Xấp xỉ hàm số: Ở gần điểm tiếp xúc, tiếp tuyến có thể coi như một xấp xỉ tuyến tính của hàm số.
Khoa học máy tính
Tối ưu hóa: Nhiều thuật toán tối ưu hóa sử dụng khái niệm đạo hàm để tìm giá trị cực đại hoặc cực tiểu của một hàm số.
Học máy: Phương pháp gradient descent, một thuật toán học máy phổ biến, dựa trên việc tính toán gradient (đạo hàm) của hàm mất mát để tìm giá trị tối ưu của các tham số.
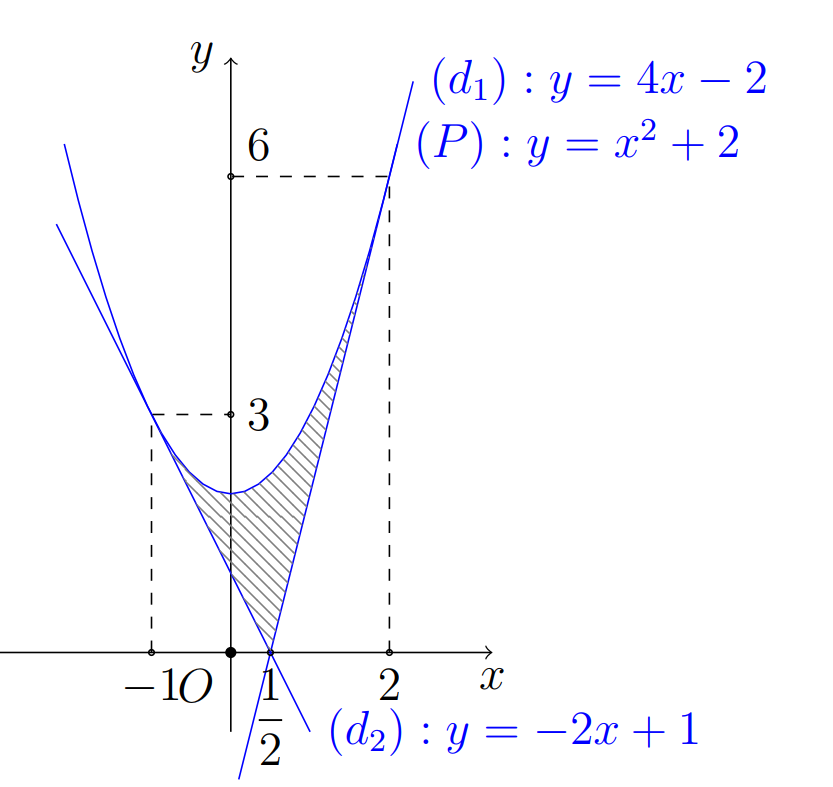
Phương trình đường tiếp tuyếnBài 1 (dễ)
Viết phương trình đường tiếp tuyến của đồ thị hàm số y = x² tại điểm có hoành độ x = 2.
Bài 2 (trung bình)
Viết phương trình đường tiếp tuyến của đồ thị hàm số y = x³ - 3x + 2 tại điểm có hoành độ x = 1.
Bài 3 (khó)
Tìm tất cả các giá trị của m để đường thẳng y = mx + 2 cắt đồ thị hàm số y = x³ - 3x² + 1 tại ba điểm phân biệt.
Bài 4 (nâng cao)
Cho hàm số y = (x² - 2x + 2)/(x - 1). Tìm điểm M trên đồ thị hàm số sao cho tiếp tuyến tại M vuông góc với đường thẳng y = x.
Lời giải chi tiết:
Mình sẽ cung cấp lời giải chi tiết cho bài 1 và 2, còn bài 3 và 4 sẽ để bạn tự làm và kiểm tra đáp án nhé.
Bài 1:
Tính đạo hàm: y' = 2x.
Tại x = 2, ta có y'(2) = 4 và y(2) = 4.
Vậy phương trình đường tiếp tuyến là y = 4(x - 2) + 4 hay y = 4x - 4.
Bài 2:
Tính đạo hàm: y' = 3x² - 3.
Tại x = 1, ta có y'(1) = 0 và y(1) = 0.
Vậy phương trình đường tiếp tuyến là y = 0(x - 1) + 0 hay y = 0.
Trên đây là các thông tin về chủ đề phương trình tiếp tuyến, hi vọng các bạn đã có cho mình thông tin hữu ích.